| Applies To | |||
| Product(s): | Microstran | ||
| Version(s): | V8i | ||
| Environment: | N/A | ||
| Area: | Dynamic Analysis | ||
| Original Author: | Richard Collins | ||
What Does Microstran Dynamic Analysis Do?
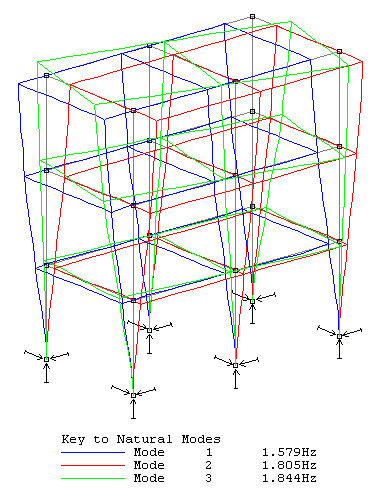
The first step in dynamic analysis is the determination of the frequencies and shapes of the natural vibration modes. In a 3-D structure there are three dynamic degrees of freedom (DDOF) for every unrestrained node with non-zero mass and there is potentially a natural vibration mode for each DDOF. Thus, there may be hundreds of potential vibration modes in a typical structure, but usually, it is only a small number of vibration modes with the lowest frequencies that are of interest. In a multi-storey building, for example, it might be only a few in each of two horizontal directions, plus one or two torsional modes that have to be considered.
The vibration mode shapes are normalized. This means that the largest value in each tabulated mode shape is +1.0. Determining the natural mode shapes and frequencies does not provide any quantitative information about the response of the structure to excitation, but in some cases it may be sufficient to know what the natural frequencies are so they can be avoided. For example, if dynamic analysis shows that the lowest natural frequency of a structure supporting a vibrating machine almost coincides with the frequency of excitation, there would be a problem. It may then be possible to stiffen the supporting structure, thereby increasing the natural frequency so that it lies outside the troublesome range.
The first three natural vibration modes are shown for a simple unbraced building frame in the diagram below.
What's the Difference Between Lumped and Consistent Mass?
When dynamic analysis is initiated the following dialog box appears:
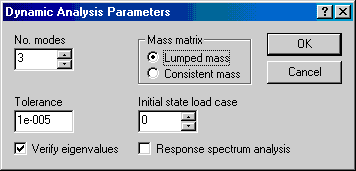
You may choose between lumped mass (the default) and consistent mass. With lumped mass, Microstran uses the simplifying assumption that all mass is concentrated at nodes, whereas with consistent mass, a more accurate formulation is used. The effect of this option is discussed below with respect to a simply supported beam.
Case 1a - No Intermediate Nodes - Lumped Mass
In Case 1a, with lumped mass, half of the mass of the beam is assumed to be concentrated at each node. Although the number of modes selected was three, only one was computed because, for lumped mass, this structure has only one dynamic degree of freedom (DDOF). This mode is the vibration of the beam in the direction of the longitudinal axis. The error in determination of this frequency is about -10% and no transverse modes are detected.

Case 1b - No Intermediate Nodes - Consistent Mass
In Case 1b, consistent mass was selected and now, the dynamic analysis finds two transverse modes with frequencies below that of the axial mode. The frequencies of these three modes are determined with errors of 11%, 27%, and 10%, respectively (the accuracy is best for mode shapes without points of inflexion).

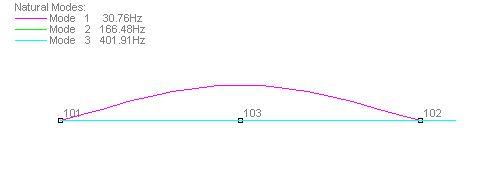
Case 2a - One Intermediate Node - Lumped Mass
In Case 2a (lumped mass), there is one intermediate node and it is assumed to have half the mass of the beam with the support nodes having one quarter each. The first transverse mode is found with an error of -1%, but the second transverse mode is not found at all. The second mode is the axial mode (error -3%) and the third mode found is actually the second axial mode.
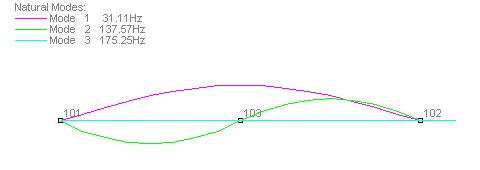
Case 2b - One Intermediate Node - Consistent Mass
Case 2b, with one intermediate node and consistent mass determines the first three modes with errors of 0.4%, 11%, and 2.5%, respectively.
Case 3a - Three Intermediate Nodes - Lumped Mass
Case 3a, with three intermediate nodes, provides frequencies that for practical purposes are exact (errors of 0.03%, 1%, and 0.7%).
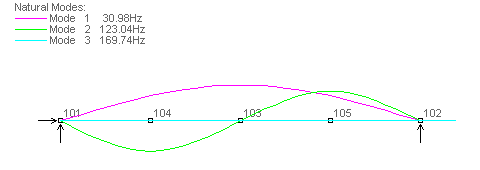
Case 3b - Three Intermediate Nodes - Consistent Mass
Case 3b, with consistent mass, provides a slight improvement in accuracy over Case 3a.
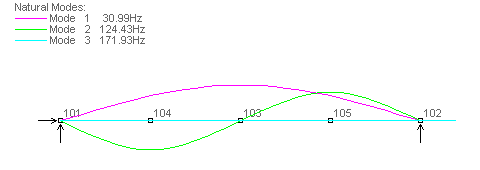
Summary
In deciding whether to use lumped mass or consistent mass you should consider the type of structure you are analysing, how it has been modelled, and the shape of the natural modes that are of primary interest.
Generally, use lumped mass:
- For models with many nodes.
- When modes of interest do not involve transverse displacement of members between nodes.
Generally, use consistent mass:
- For models with few nodes.
- When modes of interest do involve transverse displacement of members between nodes.
What is Response Spectrum Analysis?
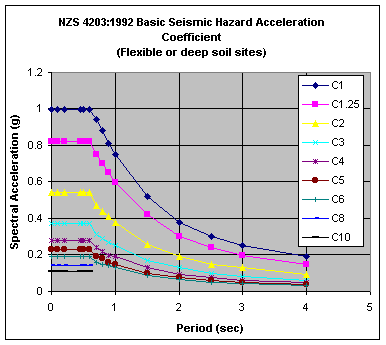
Response spectrum analysis (RSA) is a procedure for computing the statistical maximum response of a structure to a base excitation (or earthquake). Each of the vibration modes that are considered may be assumed to respond independently as a single-degree-of-freedom system. Design codes specify response spectra which determine the base acceleration applied to each mode according to its period (the number of seconds required for a cycle of vibration). The diagram below shows the Basic Seismic Hazard Acceleration Coefficient specified in NZS 4203 for deep soil sites (the most severe site category). Each curve represents a different ductility factor. The design response spectrum is obtained by multiplying these curves by a structural performance factor, a risk factor, a zone factor, and limit state factor. Other earthquake loading codes have similar provisions. Click here if you want to download a Microsoft Excel spreadsheet file containing Australian and New Zealand design code response spectra (Spectra.xls - 35K).
Having determined the response of each vibration mode to the excitation, it is necessary to obtain the response of the structure by combining the effects of each vibration mode. Because the maximum response of each mode will not necessarily occur at the same instant, the statistical maximum response, where damping is zero, is taken as the square root of the sum of the squares (SRSS) of the individual responses.
Response spectrum analysis produces a set of results for each earthquake load case which is really in the nature of an envelope. It is apparent from the calculation method, that all results will be absolute values - they are all positive. Each value represents the maximum absolute value of displacement, moment, shear, etc. that is likely to occur during the event which corresponds to the input response spectrum. Care must be taken when using these values for member design to consider the negative of each value as well. This is done most conveniently by including two design load cases for each earthquake load case, one with the RSA results factored by 1.0 and the other with them factored by -1.0.
See Also
RAM Frame - Dynamic Modal Analysis FAQ
RAM Elements Dynamic Modal Analysis FAQ
